三题,知足了。
12 分,600+ 名
题目
T1. 二进制矩阵中的特殊位置
题目
给你一个大小为 rows x cols 的矩阵 mat,其中 mat[i][j] 是 0 或 1,请返回 矩阵 mat 中特殊位置的数目 。
特殊位置 定义:如果 mat[i][j] == 1 并且第 i 行和第 j 列中的所有其他元素均为 0(行和列的下标均 从 0 开始 ),则位置 (i, j) 被称为特殊位置。
示例 1:
输入:mat = [[1,0,0], [0,0,1], [1,0,0]] 输出:1 解释:(1,2) 是一个特殊位置,因为 mat[1][2] == 1 且所处的行和列上所有其他元素都是 0
示例 2:
输入:mat = [[1,0,0], [0,1,0], [0,0,1]] 输出:3 解释:(0,0), (1,1) 和 (2,2) 都是特殊位置
示例 3:
输入:mat = [[0,0,0,1], [1,0,0,0], [0,1,1,0], [0,0,0,0]] 输出:2
示例 4:
输入:mat = [[0,0,0,0,0], [1,0,0,0,0], [0,1,0,0,0], [0,0,1,0,0], [0,0,0,1,1]] 输出:3
提示:
rows == mat.lengthcols == mat[i].length1 <= rows, cols <= 100mat[i][j]是0或1
题解思路
- 遍历行,记录这行里的哪些列可能入选
- 遍历候选列,统计结果
- 其他思路
- 三层循环
- 深度优先
参考代码
public int numSpecial(int[][] mat) {
List<Integer> cols = new ArrayList<>();
for (int[] row : mat) {
int cnt = 0, colIndex = -1;
for (int j = 0; j < mat[0].length && cnt <= 1; j++) {
if (row[j] == 1) {
cnt++;
colIndex = j;
}
}
if (cnt == 1) cols.add(colIndex);
}
int res = 0;
for (int j : cols) {
int cnt = 0;
for (int[] row : mat) {
if (row[j] == 1) cnt++;
}
if (cnt == 1) res++;
}
return res;
}
复杂度分析
- 时间复杂度:
O(rows * cols) - 空间复杂度:
O(cols)
T2. 统计不开心的朋友
题目
给你一份 n 位朋友的亲近程度列表,其中 n 总是 偶数 。
对每位朋友 i,preferences[i] 包含一份 按亲近程度从高到低排列 的朋友列表。换句话说,排在列表前面的朋友与 i 的亲近程度比排在列表后面的朋友更高。每个列表中的朋友均以 0 到 n-1 之间的整数表示。
所有的朋友被分成几对,配对情况以列表 pairs 给出,其中 pairs[i] = [xi, yi] 表示 xi 与 yi 配对,且 yi 与 xi 配对。
但是,这样的配对情况可能会是其中部分朋友感到不开心。在 x 与 y 配对且 u 与 v 配对的情况下,如果同时满足下述两个条件,x 就会不开心:
x与u的亲近程度胜过x与y,且u与x的亲近程度胜过u与v
返回 不开心的朋友的数目 。
示例 1:
输入:n = 4, preferences = [[1, 2, 3], [3, 2, 0], [3, 1, 0], [1, 2, 0]], pairs = [[0, 1], [2, 3]] 输出:2 解释: 朋友 1 不开心,因为: - 1 与 0 配对,但 1 与 3 的亲近程度比 1 与 0 高,且 - 3 与 1 的亲近程度比 3 与 2 高。 朋友 3 不开心,因为: - 3 与 2 配对,但 3 与 1 的亲近程度比 3 与 2 高,且 - 1 与 3 的亲近程度比 1 与 0 高。 朋友 0 和 2 都是开心的。
示例 2:
输入:n = 2, preferences = [[1], [0]], pairs = [[1, 0]] 输出:0 解释:朋友 0 和 1 都开心。
示例 3:
输入:n = 4, preferences = [[1, 3, 2], [2, 3, 0], [1, 3, 0], [0, 2, 1]], pairs = [[1, 3], [0, 2]] 输出:4
提示:
2 <= n <= 500n是偶数preferences.length == npreferences[i].length == n - 10 <= preferences[i][j] <= n - 1preferences[i]不包含ipreferences[i]中的所有值都是独一无二的pairs.length == n/2pairs[i].length == 2xi != yi0 <= xi, yi <= n - 1- 每位朋友都 恰好 被包含在一对中
题解思路
- 语文题~
- 提前准备哈希映射
- 注意别算重复了
参考代码
public int unhappyFriends(int n, int[][] preferences, int[][] pairs) {
Map<Integer, Map<Integer, Integer>> pre = new HashMap<>(); // (x, (each, index))
for (int i = 0; i < n; i++) {
Map<Integer, Integer> pp = new HashMap<>();
for (int j = 0; j < n - 1; j++) {
pp.put(preferences[i][j], j);
}
pre.put(i, pp);
}
Map<Integer, Integer> map = new HashMap<>();
for (int[] p : pairs) {
map.put(p[0], p[1]);
map.put(p[1], p[0]);
}
int cnt = 0;
for (int x = 0; x < n; x++) {
int y = map.get(x);
for (int u = 0; u < n; u++) {
if (u == x || u == y) continue;
int v = map.get(u);
// 对 x
// 在 x 中:u 在 y 前
// 在 u 中:x 在 v 前
Map<Integer, Integer> xMap = pre.get(x);
Map<Integer, Integer> uMap = pre.get(u);
if (xMap.get(u) < xMap.get(y) && uMap.get(x) < uMap.get(v)) {
cnt++;
break; // 不开心的原因一个即可
}
}
}
return cnt;
}
复杂度分析
- 时间复杂度:
O(n^2) - 空间复杂度:
O(n^2)
T3. 连接所有点的最小费用
题目
给你一个points 数组,表示 2D 平面上的一些点,其中 points[i] = [xi, yi] 。
连接点 [xi, yi] 和点 [xj, yj] 的费用为它们之间的 曼哈顿距离 :|xi - xj| + |yi - yj| ,其中 |val| 表示 val 的绝对值。
请你返回将所有点连接的最小总费用。只有任意两点之间 有且仅有 一条简单路径时,才认为所有点都已连接。
示例 1:
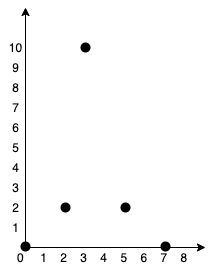
输入:points = [[0,0],[2,2],[3,10],[5,2],[7,0]] 输出:20 解释:我们可以按照上图所示连接所有点得到最小总费用,总费用为 20 。 注意到任意两个点之间只有唯一一条路径互相到达。
示例 2:
输入:points = [[3,12],[-2,5],[-4,1]] 输出:18
示例 3:
输入:points = [[0,0],[1,1],[1,0],[-1,1]] 输出:4
示例 4:
输入:points = [[-1000000,-1000000],[1000000,1000000]] 输出:4000000
示例 5:
输入:points = [[0,0]] 输出:0
提示:
1 <= points.length <= 1000-106 <= xi, yi <= 106- 所有点
(xi, yi)两两不同。
题解思路
- 连接最近的点,优先级队列解决
- 最后可能有好几堆各自为战,并查集解决
- 赛后才知道,这是 Kruskal 算法
参考代码
// 连最近的点
// union set
public int minCostConnectPoints(int[][] points) {
int n = points.length;
if (n == 1) return 0;
// 建模 {i, j, distance},距离小者先出
Queue<int[]> queue = new PriorityQueue<>(Comparator.comparingInt(a -> a[2]));
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (i == j) continue;
int dis = dis(points, i, j);
queue.add(new int[]{i, j, dis});
}
}
int sum = 0;
UnionFind uf = new UnionFind(n);
// 最后只有一个大集体
while (uf.count > 1) {
int[] ele = queue.remove();
int i = ele[0], j = ele[1], dis = ele[2];
if (uf.union(i, j)) sum += dis; // 若未连,才能连接
}
return sum;
}
private int dis(int[][] arr, int i, int j) {
int[] a = arr[i], b = arr[j];
return Math.abs(a[0] - b[0]) + Math.abs(a[1] - b[1]);
}
class UnionFind {
int count = 0;
private int[] parent;
public UnionFind(int n) {
count = n;
parent = new int[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
}
}
public boolean union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ) return false;
parent[rootP] = rootQ;
count--;
return true;
}
public int find(int p) {
int root = p;
while (root != parent[root])
root = parent[root];
while (p != parent[p]) {
int x = p;
p = parent[p];
parent[x] = root;
}
return root;
}
}
复杂度分析
- 时间复杂度:
O(n^2) - 空间复杂度:
O(n^2)
T4. 检查字符串是否可以通过排序子字符串得到另一个字符串
题目
给你两个字符串 s 和 t ,请你通过若干次以下操作将字符串 s 转化成字符串 t :
- 选择
s中一个 非空 子字符串并将它包含的字符就地 升序 排序。
比方说,对下划线所示的子字符串进行操作可以由 "14234" 得到 "12344" 。
如果可以将字符串 s 变成 t ,返回 true 。否则,返回 false 。
一个 子字符串 定义为一个字符串中连续的若干字符。
示例 1:
输入:s = "84532", t = "34852" 输出:true 解释:你可以按以下操作将 s 转变为 t : "84532" (从下标 2 到下标 3)-> "84352" "84352" (从下标 0 到下标 2) -> "34852"
示例 2:
输入:s = "34521", t = "23415" 输出:true 解释:你可以按以下操作将 s 转变为 t : "34521" -> "23451" "23451" -> "23415"
示例 3:
输入:s = "12345", t = "12435" 输出:false
示例 4:
输入:s = "1", t = "2" 输出:false
提示:
s.length == t.length1 <= s.length <= 105s和t都只包含数字字符,即'0'到'9'。
题解思路
- 据说测试用例不足
- 学习自 坑神的代码
- 「两两交换」的「向后冒泡」
- 若某数字后面有大于它的,则不可向后继续冒泡
参考代码
public boolean isTransformable(String s, String t) {
char[] sarr = s.toCharArray();
char[] tarr = t.toCharArray();
int n = sarr.length;
Stack<Integer>[] pos = new Stack[10]; // 记录每个数字的位置
for (int v = 0; v <= 9; v++)
pos[v] = new Stack<>();
for (int i = 0; i < n; i++)
pos[sarr[i] - '0'].push(i); // 大的在栈顶
// 从后向前
for (int i = n - 1; i >= 0; i--) {
int d = tarr[i] - '0';
if (pos[d].isEmpty()) return false;
// 当前数字 d 之后,不应该有比它大的数
// 否则会阻拦「向后冒泡」
for (int j = d + 1; j < 10; j++)
if (!pos[j].isEmpty() && pos[j].peek() > pos[d].peek())
return false;
pos[d].pop(); // 能够换到 t[i] 位置
}
return true;
}
复杂度分析
- 时间复杂度:
O(n) - 空间复杂度:
O(n)
赛后复盘
- T1 希望减少一些时间复杂度,差点还罚时了,卡了好久。其实深度优先或三层循环就完事了
- T2 无脑模拟,比赛时总担心有陷阱,题意也是反复读了好几遍。属于模拟的解法,再配合
Map降到O(1)查找,仅此而已 - T3 一开始是写错方向了,WA 了一次才知道:两堆点没连在一起。果断转并查集,稳定输出
- T4 比赛思考应该是逆序对的问题,时间不够了,后续再看题解吧
- 思路很巧妙,关键点还是在「两两交换」的「向后冒泡」
总体上自己是满意的,思考的过程还比较清晰,代码输出也更稳定了,不会出现一些低级错误。
测试用例的能力还是需要提高,现在甚至都懒得去造,其实这是一个非常好的锻炼更全局思维的方法,也是编程的必备素质。