本周周赛出的挺好的,每道题都需要在理解的基础上稍微转个弯。无奈 T3,T4 赛中没做出来,一闪而过的思路没有坚持,总想着一步到位:该了您内。
7 分,1100+ 名
题目
T1. 圆形赛道上经过次数最多的扇区
题目
给你一个整数
n和一个整数数组rounds。有一条圆形赛道由n个扇区组成,扇区编号从1到n。现将在这条赛道上举办一场马拉松比赛,该马拉松全程由m个阶段组成。其中,第i个阶段将会从扇区rounds[i - 1]开始,到扇区rounds[i]结束。举例来说,第1阶段从rounds[0]开始,到rounds[1]结束。请你以数组形式返回经过次数最多的扇区,按扇区编号 升序 排列。
注意,赛道按扇区编号升序逆时针形成一个圆(请参见第一个示例)。
示例 1
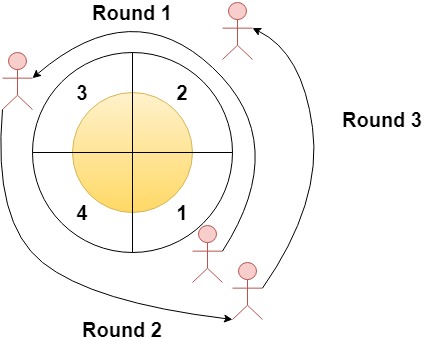
输入:n = 4, rounds = [1,3,1,2]
输出:[1,2]
解释:本场马拉松比赛从扇区 1 开始。经过各个扇区的次序如下所示:
1 --> 2 --> 3(阶段 1 结束)
--> 4 --> 1(阶段 2 结束)
--> 2(阶段 3 结束,即本场马拉松结束)
其中,扇区 1 和 2 都经过了两次,它们是经过次数最多的两个扇区。
扇区 3 和 4 都只经过了一次。
示例 2
输入:n = 2, rounds = [2,1,2,1,2,1,2,1,2]
输出:[2]
示例 3
输入:n = 7, rounds = [1,3,5,7]
输出:[1,2,3,4,5,6,7]
提示
2 <= n <= 1001 <= m <= 100rounds.length == m + 11 <= rounds[i] <= nrounds[i] != rounds[i + 1],其中0 <= i < m
题解思路
- 题意:
rounds(个人习惯,改为arr)为接力棒的人所在位置- 从
arr[0]开始跑,到ax = arr[n - 1]结束,求经过最多的区域
- 从
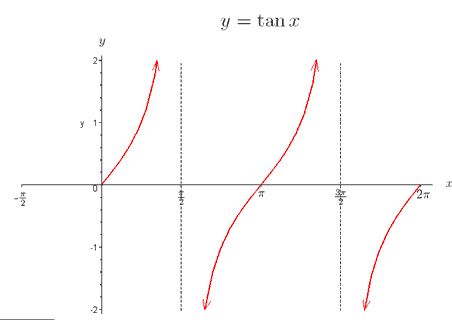
- 跑过的扇区,形如
y = tan(x)的曲线arr[0]即与Y轴交点(0, arr[0]),开始向上跑- 最终会跑到与
x = n - 1纵线的交点(n - 1, arr[n - 1])结束 - 中间所有从底部
1到顶部n的上坡路次数都相同 - 只需关注头尾两段斜坡
- 头斜坡
[arr[0], n],尾斜坡[1, arr[n - 1]]
参考代码
public List<Integer> mostVisited(int n, int[] arr) {
int a0 = arr[0], ax = arr[arr.length - 1]; // 头、尾端点
if (a0 == ax) return Collections.singletonList(a0); // a0 恰为重叠处
List<Integer> res = new ArrayList<>();
if (a0 > ax) { // 无重叠,两段都算
for (int v = 1; v <= ax; v++) res.add(v);
for (int v = a0; v <= n; v++) res.add(v);
return res;
}
// a0 < ax,有重叠,只算重叠部分
for (int v = a0; v <= ax; v++) res.add(v);
return res;
}
复杂度分析
- 时间复杂度:
O(n),n为 参数n,而非arr.length - 空间复杂度:
O(1),不计返回值
T2. 你可以获得的最大硬币数目
题目
有 3n 堆数目不一的硬币,你和你的朋友们打算按以下方式分硬币:
- 每一轮中,你将会选出 任意 3 堆硬币(不一定连续)。
- Alice 将会取走硬币数量最多的那一堆。
- 你将会取走硬币数量第二多的那一堆。
- Bob 将会取走最后一堆。
- 重复这个过程,直到没有更多硬币。
给你一个整数数组
piles,其中piles[i]是第i堆中硬币的数目。返回你可以获得的最大硬币数目。
示例 1:
输入:piles = [2,4,1,2,7,8]
输出:9
解释:选出 (2, 7, 8) ,Alice 取走 8 枚硬币的那堆,你取走 7 枚硬币的那堆,Bob 取走最后一堆。
选出 (1, 2, 4) , Alice 取走 4 枚硬币的那堆,你取走 2 枚硬币的那堆,Bob 取走最后一堆。
你可以获得的最大硬币数目:7 + 2 = 9.
考虑另外一种情况,如果选出的是 (1, 2, 8) 和 (2, 4, 7) ,你就只能得到 2 + 4 = 6 枚硬币,这不是最优解。
示例 2:
输入:piles = [2,4,5]
输出:4
示例 3:
输入:piles = [9,8,7,6,5,1,2,3,4]
输出:18
提示:
3 <= piles.length <= 10^5piles.length % 3 == 01 <= piles[i] <= 10^4
题解思路
- 每次都选最大的两个 + 最小的一个
- 给 Bob 那个倒霉蛋留
n个最小的
- 给 Bob 那个倒霉蛋留
- Alice 选每次的最大,则我们取第二大最优(千年老二?
- 答案为 从大到小,间隔取:贪心思想
参考代码
public int maxCoins(int[] arr) {
Arrays.sort(arr);
int sum = 0, n = arr.length / 3;
for (int i = arr.length - 2, cnt = 0; cnt < n; i -= 2, cnt++)
sum += arr[i];
return sum;
}
复杂度分析
- 时间复杂度:
O(nlog(n)) - 空间复杂度:
O(1)
T3. 查找大小为 M 的最新分组
题目
给你一个数组
arr,该数组表示一个从1到n的数字排列。有一个长度为n的二进制字符串,该字符串上的所有位最初都设置为0。在从
1到n的每个步骤i中(假设二进制字符串和arr都是从1开始索引的情况下),二进制字符串上位于位置arr[i]的位将会设为1。给你一个整数
m,请你找出二进制字符串上存在长度为m的一组1的最后步骤。一组1是一个连续的、由1组成的子串,且左右两边不再有可以延伸的1。返回存在长度 恰好 为
m的 一组1的最后步骤。如果不存在这样的步骤,请返回-1。
示例 1:
输入:arr = [3,5,1,2,4], m = 1
输出:4
解释:
步骤 1:"00100",由 1 构成的组:["1"]
步骤 2:"00101",由 1 构成的组:["1", "1"]
步骤 3:"10101",由 1 构成的组:["1", "1", "1"]
步骤 4:"11101",由 1 构成的组:["111", "1"]
步骤 5:"11111",由 1 构成的组:["11111"]
存在长度为 1 的一组 1 的最后步骤是步骤 4 。
示例 2:
输入:arr = [3,1,5,4,2], m = 2
输出:-1
解释:
步骤 1:"00100",由 1 构成的组:["1"]
步骤 2:"10100",由 1 构成的组:["1", "1"]
步骤 3:"10101",由 1 构成的组:["1", "1", "1"]
步骤 4:"10111",由 1 构成的组:["1", "111"]
步骤 5:"11111",由 1 构成的组:["11111"]
不管是哪一步骤都无法形成长度为 2 的一组 1 。
示例 3:
输入:arr = [1], m = 1
输出:1
示例 4:
输入:arr = [2,1], m = 2
输出:2
提示:
n == arr.length1 <= n <= 10^51 <= arr[i] <= narr中的所有整数 互不相同1 <= m <= arr.length
题解思路
- 起始全
0,最终全1 - 求「最后一步」,倒序反推:从全
1到 全0 - 每次
arr[i]理解为「因一个0,将原来连续的多个1分隔开了」 - 注意:分割点
0刚好在连续1的头或尾 - 补充:不用
TreeMap也可用其他方式(如二分),从keys中找到比指定值p小的key
参考代码
public int findLatestStep(int[] arr, int m) {
int n = arr.length;
if (m == n) return n;
TreeMap<Integer, Integer> map = new TreeMap<>(); // (from, to)
map.put(1, n); // [1, n] 整段全 1
for (int i = n - 1; i >= 0; i--) {
int p = arr[i]; // 分割点
// 找比 p 小的第一个 key
int from = map.floorKey(p); // 一定存在
int to = map.get(from);
if (p > from) { // 包括 p == to
if (p - from == m) return i;
map.put(from, p - 1); // [from, p - 1]
}
if (p < to) { // 包括 p == from
if (to - p == m) return i;
map.put(p + 1, to); // [p + 1, to]
}
}
return -1;
}
复杂度分析
- 时间复杂度:
O(nlog(n)),查找key为log(n) - 空间复杂度:
O(n)
T4. 石子游戏 V
题目
几块石子 排成一行 ,每块石子都有一个关联值,关联值为整数,由数组
stoneValue给出。游戏中的每一轮:
- Alice 会将这行石子分成两个 非空行(即,左侧行和右侧行);
- Bob 负责计算每一行的值,即此行中所有石子的值的总和。
- Bob 会丢弃值最大的行,Alice 的得分为剩下那行的值(每轮累加)。
如果两行的值相等,Bob 让 Alice 决定丢弃哪一行。下一轮从剩下的那一行开始。
只 剩下一块石子 时,游戏结束。Alice 的分数最初为
0。返回 Alice 能够获得的最大分数 。
示例 1:
输入:stoneValue = [6,2,3,4,5,5]
输出:18
解释:在第一轮中,Alice 将行划分为 [6,2,3],[4,5,5] 。左行的值是 11 ,右行的值是 14 。Bob 丢弃了右行,Alice 的分数现在是 11 。
在第二轮中,Alice 将行分成 [6],[2,3] 。这一次 Bob 扔掉了左行,Alice 的分数变成了 16(11 + 5)。
最后一轮 Alice 只能将行分成 [2],[3] 。Bob 扔掉右行,Alice 的分数现在是 18(16 + 2)。游戏结束,因为这行只剩下一块石头了。
示例 2:
输入:stoneValue = [7,7,7,7,7,7,7]
输出:28
示例 3:
输入:stoneValue = [4]
输出:0
提示:
1 <= stoneValue.length <= 5001 <= stoneValue[i] <= 10^6
题解思路
- 题意:切分数组,统计少的那一半,递归累计
- 怎么切,都试试:对分割点
p的for迭代尝试 - 怎么算切的好:看看继续往下切的最优能得多少,即:依赖于更细粒度的切分
- 动态规划,适合 Bottom-Up
- 实现可选:深度优先 + 记忆化
- 技巧:前缀和
pre空间换时间,方便计算某段数组和
参考代码
public int stoneGameV(int[] arr) {
int n = arr.length;
if (n == 1) return 0;
if (n == 2) return Math.min(arr[0], arr[1]);
// 前缀和 presum
int[] pre = new int[n + 1];
for (int i = 0; i < n; i++)
pre[i + 1] = pre[i] + arr[i];
return dfs(pre, 0, n - 1, new int[n][n]);
}
private int dfs(int[] pre, int l, int r, int[][] memo) {
if (l >= r) return 0;
if (memo[l][r] > 0) return memo[l][r];
int max = 0;
// [l, p, r]
for (int p = l; p < r; p++) {
int lp = pre[p + 1] - pre[l]; // [l, p]
int pr = pre[r + 1] - pre[p + 1]; // [p + 1, r]
if (lp > pr) { // 左段大
max = Math.max(max, pr + dfs(pre, p + 1, r, memo));
} else if (lp < pr) { // 右段大
max = Math.max(max, lp + dfs(pre, l, p, memo));
} else { // 一样大
int dfs1 = dfs(pre, l, p, memo);
int dfs2 = dfs(pre, p + 1, r, memo);
max = Math.max(max, lp + Math.max(dfs1, dfs2));
}
}
return memo[l][r] = max;
}
复杂度分析
- 时间复杂度:
O(n^2),每个memo都O(1) - 空间复杂度:
O(n^2),memo的花费
赛后复盘
- T1 理解起来挺费劲,中学知识「数形结合」没白学,理解之后就好多了。暴力解法
O(mn)也是可以过的 - T2 比 T1 简单,可以作为简单题,理清贪心思想就好写了
- T3 比赛时没写出来,想的并查集,结果没并出个所以然,一闪而过的「反推」也仅仅是闪过了,白费了类似的还写过多解法的题解,可惜了
- T4 明显确定是动态规划,也是一开始想到 dfs + memo,结果嘚瑟了,非得要试试迭代,也没迭出来,赛后 dfs 十分钟提交也然并卵
总体是出的不错的一周,值得复盘与复习。
吃透一题未必就吃透一类,多多举一反三,现在的题量可以逐渐开始同类型题一起做了,专项的刻意练习,加深对算法思想、写法的体会。
后续的比赛有时间都会发上来,专项的总结也考虑发出来做个回顾。